|
We are thankful to Mr. Matsubara, President of Shinko Co., Ltd. for his contribution to the uploading of this paper.
<GemTec>
|
|
By W.R. Eulitz
|
|
Editor's Note : Dr.W.R. Eulitz, a noted physicist and mathematician is a part of the United States space team at Huntsville, Alabama, that is led by Dr. Werner Von Braun. Dr. Eulitz's study of gemology is a hobby. The proportions of the round brilliant fascinated him and led into the extensive research that culminated in this paper
The introduction of the triple-cut diamond by Peruzzi a few centuries ago caused by a sensation in the diamond-cutting industry. The fashionable language of those days, French, called the appearance of Peruzzi diamonds "brilliant", which means excellent superb, splendid, magnificent. Later, this attribute typified the stone itself: a diamond cut in Peruzzi style was simply a "brilliant".
The brilliant of today is, in principle, the same as the Peruzzi brilliant, with the only difference being that the squared format of the girdle has been rounded and the angles between the facets have been modified. The basic centro-symmetric design, crown and pavilion fashioned with a total of 58 facets, did not change.
During the centuries, the cutting industry learned by experience that the beautiful effect of a brilliant depends primarily on the inclination of the main facets (bezels and pavilion) to the girdle plane. The optimum angles, however, remained a puzzle. And even today, there is no general agreement about the proper angles. Commonly, it is considered a delicate art to cut the stone in such a way that the result is optimum beauty.
During the first three decades of this century, attempts have been made to calculate the proper proportions for the brilliant-cut diamond. But all these calculations did not provide any more brilliancy than a few practitioners obtained by intuition. Results obtained by different authors disagreed, partially because they judged brilliancy by different standards.
In 1919, Marcel Tolkowsky published a book, Diamond Design (out of print). By trial-and-error calculations, considering the critical angle as the limit for refraction and reflection, Tolkowsky arrived at proportions that are very close to what is supposed to be the perfect brilliant cut by long-experienced diamond cutters striving for maximum beauty, rather than maximum weight retention. His figures are accepted in this country by the GIA as the standard proportions of a perfect brilliant. They are, with the other suggestions in parenthesis for comparison: pavilion angel α=40.75° (40.8°); crown angle, β=34.5° (33.2); table diameter, 53%(56%); pavilion height, 43.1%(43.2%); crown height, 16.2%(14.4%); total depth, 60.3%(58.6%). Actually, all these figures vary widely, because almost every cutters claims his products are the ultimate of the art. This widespread disagreement stimulated a new study of the problem from another point of view.
It is well known that the beautiful appearance of a brilliant is the result of a special effect of light, or, more precisely, it is a combination of the quantity and quality of light reflected by the stone. A brilliant is irradiated in any imaginable direction from the outside and these light rays can enter the stone through the table as the main "window". It also is well known that all these rays change their direction when entering the stone; they are refracted.
So far, there is no particular phenomenon, because light penetrates a great number of materials and is thereby refracted. What the appearance of a brilliant-cut stone, especially diamond, makes so outstanding depends primarily on the form in which the stone is cut and in a secondary respect, on the high refractive index of diamond. A diamond cut as a flat plate with two parallel planes would never have the effect of a brilliant, although the high refractive index exists.
Hence, the primary question is: what happens to the collected light inside the stone? What are the prerequisites for light rays to be reflected to the outside in the direction to the observer? Are there any general rules that govern such an optical system, and, if so, can such rules serve to tell the degree of brilliancy of a stone from its external shape?
To discern this, we will, in the first place, consider the paths of light rays inside the stone and, subsequently, the effect toward the outside. For better understanding, the important symbols used in the following discussion may be explained beforehand.
|
편집자 주 : W.R. Eulitz박사는 저명한 물리학자이자 수학자로 Werner Von Brawn 박사가 이끄는 Alabama의 Huntsville에 있는 미국 우주단의 일원이다. Eulitz박사의 보석학 연구는 취미이다. 원형다각(brilliant)의 비율에 매료되어 이 논문에서 그 절정에 다다른 광범위한 연구에 들어갔다.
수 세기 전에 Peruzzi에 의해서 소개된 삼중연마가공 다이어먼드는 다이어먼드 연마가공 산업에 감동을 일으켰다. Peruzzi 다이어먼드의 외관을 불어로 훌륭한 최상의, 화려한, 장려한 이라는 뜻인 그 당시의 유행어로 "brilliant"라고 불렀다. 후에, 이 속성은 돌 자체를 대표하게 되었다: Peruzzi형태로 연마가공된 다이어먼드는 단순히 브릴리언트(brilliant)이었다.
오늘날의 다각원형(brilliant)는 원칙적으로 Peruzzi 다각원형과 같다. 단 하나 다른 것은 환상부의 사각형태가 둥글게 되었고 패시트(facet)들 사이의 각들이 바뀌었다. 모두 58개의 패시트들로 이루어진, 기초적인 중심 대칭적인 고안, 관부(crown)과 퍼빌리언(pavilion)은 변하지 않았다.
수 세기동안, 다각원형의 미적 효과는 본질적으로 환상부 면(girdle facet)에 대한 주 패시트들(관부와 퍼빌리언)의 경사각에 달렸다는 것을 연마가공산업계는 경험에 의해서 배웠다. 그러나, 최적의 각들은 수수께끼로 남았다. 그리고 오늘날조차도, 적절한 각들에 대한 일반적인 동의가 없다. 보통, 최적의 미가 나타나게 하는 방법으로 돌을 연마가공하는 것을 하기 어려운 예술로 간주한다.
금세기 초의 30년동안에, 다각원형 연마가공 다이어먼드에 적절한 비율들을 계산하기 위한 시도들이 있었다. 그러나 이 모든 계산들은 직관으로 구했던 소수의 견습자들보다 광휘를 전혀 더 많이 내지 못했다. 서로 다른 기준에 의해서 광휘를 판단했기 때문에 다른 창시자들에 의해서 구한 결과들은 부분적으로 동의를 얻지 못했다.
1919년, Marcel Tolkowsky는 다이어먼드 고안(Diamond design, 절판)이라는 책을 발간했다. 굴절과 반사에 대한 제한으로 임계각을 고려한 시행착오 계산법에 의해서, Tolkowsky는 최대의 중량보유보다는 최대의 미를 위하여 애쓴 오랜 경험의 다이어먼드 연마가공가들에 의해서 완벽하게 연마가공되었다고 생각되는 것과 아주 근접한 비율들에 도달했다. 그의 계산들은 GIA에 의하여 완벽한 다각원형(brilliant)를 위한 표준 비율들로서 받아들여졌다. 그들은 (괄호 안의 값들은 비교를 위한 것이다): 퍼빌리언 각 α=40.75° (40.8°); 관부 각, β=34.5° (33.2); 테이블 직경(table diameter), 53%(56%); 퍼빌리언 높이(pavilion height), 43.1%(43.2%); 관부 높이(crown height), 16.2%(14.4%); 전체 깊이, 60.3%(58.6%)이다. 거의 모든 연마가공가마다 자신의 제품들이 최고의 예술이라고 주장을 하는 관계로, 이 모든 값들은 실제로는 크게 변한다. 이렇게 만연된 의견차이는 다른 관점에서 문제를 새로 연구하도록 하는 자극제가 되었다.
다각원형의 아름다운 외관은 빛의 특정한 효과의 결과, 또는 더 정확하게는 돌에 의해서 반사되는 빛의 양과 질의 혼합에 의한 결과라는 것은 잘 알려져 있다. 다각원형은 외부로부터의 모든 가상 방향에서 빛을 받으며 이 광선들은 주 "창문"인 테이블을 통하여 돌에 들어갈 수 있다. 또한, 이 모든 광선들은 돌에 들어갈 때, 그 방향을 바꾼다 (굴절한다)는 것은 잘 알려져 있다.
지금까지는, 수 많은 재료들을 통과하고 그리고 그 때문에 굴절했기 때문에 특별한 현상은 없다. 다각원형 연마가공 돌, 특히 다이어먼드의 외관을 그렇게 뛰어나게 만든 것은 일차적으로는 돌이 연마가공된 형태 그리고 이차적인 측면으로는 다이어먼드의 높은 굴절률에 달렸다. 두 개의 평행한 면들로 이루어진 편평한 판으로 연마가공된 다이어먼드는 높은 굴절률을 지녔다고 하더라도, 결코 브릴리언트 효과를 지닐 수 없을 것이다.
그러므로, 일차적인 질문은: 돌의 안에 모여진 빛에는 어떠한 일이 일어나는가? 광선이 관찰자를 향하여 밖으로 반사되기 위한 필요조건은 무엇인가? 그런 광학계를 좌우하는 어떠한 일반적인 규칙이 있는가 그리고 그렇다면, 그런 규칙은 외부의 형상으로 돌의 광휘도(brilliancy)를 나타낼 수가 있는가?
이를 알기 위하여, 우리는 우선, 돌의 내부에서의 광선의 경로들 그리고 다음에 외부에 대한 효과를 생각할 것이다. 이해를 돕기 위하여, 다음의 논의에 사용되는 중요한 표시들에 대하여 우선 설명하고자 한다.
|
|
|
|
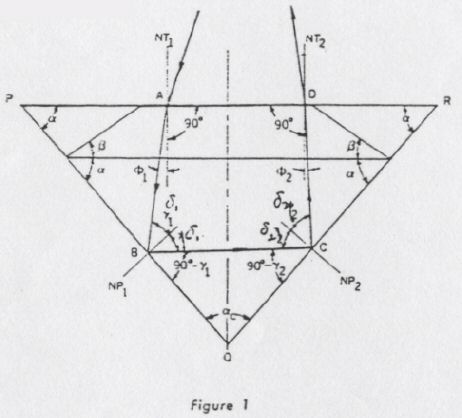
All angles are symbolized by Greek letters (Figure 1): α = pavilion angle, β = crown angle, αc = angle between the pavilion facets at the culet. These angles characterize the given brilliant cut; they are, of course, supposed to be constant for an individual stone. Angle Ø indicates the refractive angle at the table, whereby Ø1, (index 1) stands for the refractive angles at the left half of the diagram, while Ø2 (index 2) refers to the refractive angles at the right side. The angles of reflection at the pavilion facets are designated δ with indices of respective meaning.
The angles are always measured between the ray and the normal to the facet, not to the facet itself. The normal (lines vertical to the facet) are designated NT for the table, NP for the pavilion facets, and NB for the bezel facets.
In the first step of our investigation, we neglect the bezel facets and illustrate the profile of the stone by a simple triangle PQR, as shown in Figure 1.
Suppose a ray from outside enters the table at point A and is going to point B at the pavilion facet. Then, Ø1 is the refractive angle at the table, and δ1 is the angle of incidence at the pavilion facet. The law of reflection requires that the angle of reflection is equal to the angle of incidence. Thus, the ray is reflected with angle δ1 to the opposite pavilion facet at point C, being incident with angle δ2. With the same angle δ2, the ray is reflected back to the table entering with angle Ø2 in point D. This incident angle Ø2, actually, is the refractive angle for the ray leaving the stone to the outside.
Each of the three steps of the ray forms three triangles with the corners of the profile, triangles ABP, BCQ and CDR. The sum of the three angles within each triangle is 180 degrees. The angles of the normals to the facets are, of course, 90 degrees. Thus, considering triangle ABP, the angle inside the triangle at A is (90-Ø1), and the angle at B is (90-δ1). The total sum of all angles within triangle ABP is now:
|
모든 각들을 그리스어로 기호화한다 (그림 1): α = 퍼빌리언 각, β = 관부 각, αc = 큘릿(culet)에서의 퍼빌리언 패시트들 사이의 각. 이 각들은 주어진 다각원형 연마가공의 특성을 나타낸다; 물론 그들은 개개의 돌마다 일정하다고 가정한다. 각 Ø는 테이블에서의 굴절각, 그로 인하여, Ø1 (표시 1)은 도표의 왼 반쪽에서의 굴절각을 의미하며, Ø2 (표시 2)는 오른쪽에서의 굴절각을 말한다. 퍼빌리언 패시트들에서의 각들은 δ로 대응표시를 한다.
각들은 항상 광선과 (패시트 자체가 아닌) 패시트에 대한 수직선사이의 각을 측정한다. 수직선(패시트에 대하여 수직인 선들)은 테이블에 대해서는 NT로, 퍼빌리언 패시트들에 대해서는 NP 그리고 관부사면(bezel) 패시트들에 대해서는 NB로 표시한다.
조사의 첫 단계에서는, 관부사면 패시트들을 무시하며 그림. 1에서와 같이 돌의 측면을 간단한 삼각형 PQR로 나타낸다.
광선이 외부로부터 점A에서 테이블로 들어가 퍼빌리언 패시트 점B까지 간다고 가정한다. 그러면, Ø1는 테이블에서의 굴절각이고 δ1은 퍼빌리언 패시트에서의 입사각이다. 굴절의 법칙에 의하여 굴절각은 입사각과 같다. 그러므로, 광선은 각 δ1로 반대쪽 퍼빌리언 패시트의 점C에 반사되어 입사각 δ2를 이룬다. 광선은 같은 각 δ2로 테이블로 되돌아가 점D에서 각 Ø2로 들어간다. 이 입사각 Ø2는 실제로는 돌의 외부로부터 떠난 광선의 굴절각이다.
광선의 3 단계들의 각각은 돌의 측면 모서리를 지닌 3 개의 삼각형들, ABP, BCQ와 CDR를 형성한다. 각 삼각형내의 3 개의 각들의 합은 180도이다. 패시트들에 대한 수직각들은 물론 90이다. 그러므로, 삼각형 ABP을 고려하여, A에서의 삼각형의 내부의 각은 (90-Ø1)이며, B에서의 각은 (90-δ1)이다. 삼각형 ABP내의 모든 각의 합은 이제:
|
|
α + (90 - Ø1) + (90 - δ1)
=180°
or α = Ø2 + δ1
or δ2 = α ± Ø1
|
(1a)
(1b)
|
|
|
The same situation exists for the other two triangles. In triangle CDR, we have
|
같은 상황은 다른 2개의 삼각형들에도 존재한다. 삼각형 CDR에서, 우리는
|
|
α + (90 - Ø2) + (90 - δ2)
=180°
or α = Ø2 + δ2
or δ2 = α ± Ø2
|
(2a)
(2b)
|
|
|
Triangle BCQ provides
|
삼각형 BCQ는
|
|
αc + (90 - δ1) + (90 - δ2)
=180°
or α = Ø2 + δ2
|
(3a)
|
|
|
The correlation between and in triangle PQR is
|
삼각형 PQR사이와 내에서의 상관 관계는
|
|
αc + 2α = 180°
or αc = 180 - 2α
|
(3b)
|
|
|
Substituting (3b) into (3a)
|
(3b)를 (3a)에 치환하고
|
|
|
|
combing (1b) and (2b)
|
(1b)와 (2b)를 합하고
|
|
|
|
substituting (3c) for ( ) (δ1 + δ2)
|
(3c)를 ( ) (δ1 + δ2)에 치환하며
|
|
|
|
and rearranging, we finally obtain
|
그리고 재배열하면, 최종적으로
|
|
|
|
|
|
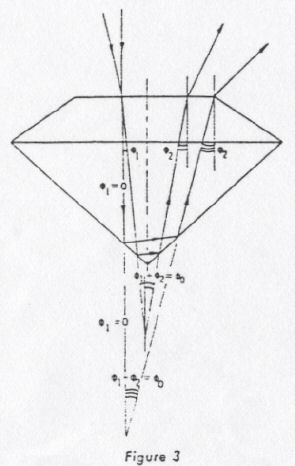
This means the sum of the angles at the table (incident refractive angle plus exit refractive angle) of any ray inside the stone that is reflected by the pavilion facets is constant and depends only on the size of the pavilion angle α. The two angles (Ø1 + Ø2) combine behind the culet to one angle, Ø0, which is a characteristic angle of the cut, and which is the same for all rays reflected inside the stone, as demonstrated in Figure 3. Equation (4a) can now be written:
|
이것은 퍼빌리언 패시트들에 의해서 반사되는 돌 내의 어떠한 광선의 테이블에서의 각들의 합(입사 굴절각 + 출사 굴절각)은 일정하며 퍼빌리언 각 α의 크기만에 달려있다는 것을 의미한다. 두 각들(Ø1 + Ø2)은 큘릿아래에서 합쳐져 연마가공 특성 각인 Ø0가 되며 그림 3에 보인 바와 같이 돌 내에서 반사되는 모든 광선들에게 같다. 식(4a)는 이제 다음과 같이 쓰여질 수 있다:
|
|
Ø0 = Ø1 + Ø2 = 4α - 180°
|
(4b)
|
|
|
We conclude from equation (4b) that Ø0 is zero if α = 45°. In this case, Ø1 and Ø2 are always equal but they have opposite sign. This means if the pavilion angle is 45°, all rays leaving the stone are parallel to the originating incident rays. For α smaller than 45°, Ø0 is becomes negative; and for α larger than 45°, Ø0 is positive. This inversion of sign is possible for the components of Ø0 also; i.e., Ø1 and Ø2. Recalling equations (1b) and (2b), we find that the angle of reflection at the pavilion δ1 = α and δ2 = α, if Ø1 or Ø2 is zero, respectively. If δ1 or δ2 is smaller than α, then, Ø1 or Ø2 is positive; if one of the two angles, δ1 or δ2, is larger than α, Ø1 or Ø2 is negative. For Ø1 or Ø2 equal to zero, the rays coincide with the normal.
|
식(4b)로부터, 만약에 α = 45°이면 Ø0는 영(zero)이라는 결론을 낼 수 있다. 이 경우에, Ø1과 Ø2는 항상 같지만, 반대부호를 지닌다. 이것은 만약에 퍼빌리언 각이 45°이면, 돌을 떠나는 모든 광선들은 처음의 입사 광선들과 평행하다는 것을 의미한다. 45°보다 작으면, Ø0는 음수가 되며; 45°보다 크면, Ø0는 양수이다. 이 부호의 역은 Ø0의 성분들 즉, Ø1과 Ø2에도 가능하다; 식(1b)과 (2b)를 되돌아 생각하면, 만약에 Ø1 또는 Ø2가 영(zero)이면, 퍼빌리언에서의 반사각은 각각 δ1 = α와 δ2 = α임을 알 수 있다. 만약에 δ1 또는 δ2가 α보다 작으면, Ø1 또는 Ø2는 양수이다; 만약에 두 개의 각들, δ1 또는 δ2,의 하나가 α보다 크면, Ø1 또는 Ø2는 음수이다. Ø1 또는 Ø2가 영(zero)일 때, 광선들은 법선과 일치한다.
|
|
|
|
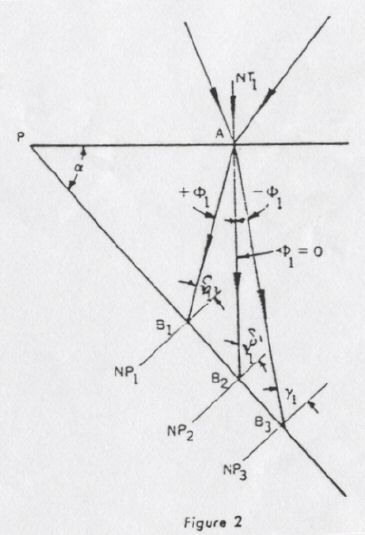
The three typical cases are illustrated in Figure 2, where only the left corner of Figure 1 is plotted. Positive Ø1 is outside the corresponding triangle AB3P; negative Ø1 is inside the triangle AB3P.
|
그림 1의 왼쪽 모서리만을 나타낸 그림 2에 3 개의 전형적인 경우들을 예시하였다. 양의(+) Ø1는 대응 삼각형 AB3P의 외부이고; 음의(-) Ø1는 삼각형 AB3P의 내부이다.
|
|
|
|
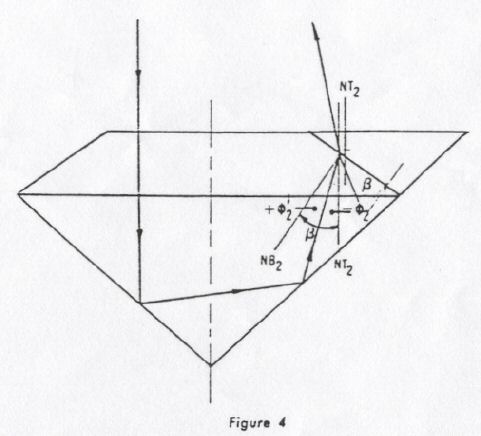
Incorporating now the crown angle β, Figure 4, it is evident that this angle has no influence on the angle Ø0 at all. We can readily read from Figure 4 that the refractive angle Ø12 at the bezel facet has a very simple correlation to the corresponding angle Ø2 at the table.
It is, Ø12 - β = Ø2
and if we add the angle Ø1 for the incident ray to both sides of the equation, we obtain
|
이제, 그림 4의 관부 각 β를 혼합하는데, 이 각은 각 Ø0에 아무런 영향도 주지 않는다는 증거이다. 우리는 그림 4에서 관부사면에서의 굴절각 Ø12는 테이블에서의 대응각 Ø2와 아주 간단한 관계를 지니고 있다는 것을 즉시 알 수 있다.
즉, Ø12 - β = Ø2
그리고 만약에 식의 양쪽에 입사광선의 각 Ø1을 더하면, 다음을 얻는다
|
|
Ø1 + Ø12 - β = Ø1 + Ø2 = Ø0
|
(5a)
|
|
|
Referring to equation (4b), we accordingly combine the two angles, Ø1 and Ø1 of the ray to one angle Ø10 and equation (5a) becomes
|
식(4b)를 참조하고, 따라서 Ø1과 하나의 각 Ø10에 대한 광선 Ø1 두 각들을 합치면 식 (5a)는 다음과 같이 된다
|
|
Ø10 - β = Ø1 + Ø12 - β = Ø0
|
(5b)
|
|
|
The two components (Ø1 + Ø2) and (Ø1 + Ø12), of each the total angles, Ø0 + Ø10 are of fundamental importance. One of them characterizes the refractive angle of the incident ray; the other one characterizes that of the departing ray. In the following, we will consider the angle with index 1 as that of the incident ray, the other one with index 2 is for the departing ray. The latter is of primary interest because the departing (reflected) ray makes the appearance of the brilliant. We question now, which rays collected inside the stone (angle Ø1) can be reflected to the outside (angles Ø2) for a given brilliant cut, or, what is the angular margin (maximum and minimum) for rays departing from the table and from the bezel facets.
This means with reference to the formulae derived above, we have to find a correlation between the two refractive angles, Ø1 and Ø2, and the angles α and β, which characterize the geometric-optical quality of the cut. Then, the correlation has to be resolved for the exit refractive angle Ø2. In other words, the problem is: which of all possible rays that enter the stone with refractive angle Ø1 return to the table or bezel facet under such an angle Ø2 that they can escape to the outside without being totally reflected to the outside of the stone?
We recall equation (4b), which states
|
각각의 전체 각들, Ø0 + Ø10의 두 성분들 (Ø1 + Ø2)과 (Ø1 + Ø12)은 근본적으로 중요하다. 이들 중의 하나는 입사광선의 굴절각의 특성을 나타난다; 다음에서, 입사광선의 굴절각으로 표시 1인 각, 표시 2인 다른 것은 출사광선인 것으로 생각할 것이다. 출사(굴절된) 광선이 다각원형의 외관을 만들기 때문에 후자가 일차적인 관심거리이다. 이제 우리의 의문은 주어진 다각원형 연마가공에서, 돌 내부(각 Ø1)에 모인 광선들이 외부(각 Ø2)로 반사될 수 있을 것인가 또는 테이블과 관부사면들을 떠나는 광선들의 각도적인 여유(최대와 최소)는 얼마인가이다.
이것은 위에서 유도한 공식들에 대한 것을 의미하며, 우리는 연마가공의 기하학적인 광학적 질을 특성화하는 두 개의 굴절각들 Ø1과 Ø2, 그리고 각 α와 β사이의 상호관계를 찾아야 한다. 그리고 나서, 출구 굴절각 Ø2에 대한 상호관계를 해결해야 한다. 다시 말하면, 문제는: 굴절각 Ø1로 돌에 들어갈 가능성이 있는 모든 광선들 중에서, 돌의 외부로 완전히 반사되지 않고 외부로 탈출할 수 있는 각 Ø2와 같은 각 아래에서 테이블이나 관부사면으로 되돌아가는 것은 어느 광선인가?
식 (4b)을 상기하여 기술하면,
|
|
|
|
and from equation (5a) we have
|
그리고 식 (5a)로부터 다음을 얻는다.
|
|
Ø1 + Ø12 = Ø0 + β
= 4α + β - 180°
|
|
|
|
The first of the two equations refers by definition to table reflections. For an angle of β = 0°, the second equation is identical with the first one. Thus, the first equation can be considered a special case of the other equation; and β has the general meaning of the inclination angle, with reference to the girdle plane, of any facet (also star and upper girdle facets), which is met by a ray from inside the stone. For a ray striking the table from inside, β is zero.
From this point of view, the left sides of the two equations above can be considered equal, and the two equations can be combined to one generally valid equation:
|
두 식들 중의 첫째는 테이블 반사들에 대한 정의로서 말한다. β = 0°인 각에 대하여, 둘째 식은 첫째와 같다. 그러므로, 첫째 식은 다른 식의 특별한 경우로 고려될 수 있다; 그리고 β는 어떤 패시트(스타와 환상부 상부의 패시트들도 역시)의 환상부 면에 대한 일반적인 경사각을 의미하며, 돌의 내부로부터의 광선과 마주친다. 내부로부터 테이블에 부딪치는 광선에 대해서, β는 영(zero)이다.
이 관점으로부터, 위의 두 개의 식들의 왼쪽들은 같다고 간주할 수 있으며 두 식들은 하나의 일반적으로 유효한 식으로 합쳐질 수 있다.
|
|
|
|
Resolving for Ø2
|
Ø2에 대하여 풀면,
|
|
Ø2 = 4α + β - 180° - Ø1
|
(6)
|
|
|
This is the final equation that describes completely and sufficiently the reflecting properties of a brilliant-cut diamond on the ground of the design angles α and β. For this reason, equation (6) may be designated the brilliant equation.
To discern the angular margin of all rays Ø2, which can leave a stone of design (α, β) after internal reflection, it is important to know which rays can enter the stone, or what is the possible maximum and minimum for the entering ray Ø1. As a matter of fact, Ø1 cannot be larger than the critical angle Øcr = 24.5° for diamond. Thus, Ø1 can, at first sight, vary within the interval +24.5 ≤ Ø2 ≥ -24.5 (the symbol ≤ means smaller or equal to; ≥ means larger or equal to). The same, obviously, applies to ray Ø2. If ray Ø2 is supposed to leave the stone, it has to strike the facet from inside the stone within the same interval +24.5 ≤ Ø2 ≥ -24.5. The transition of light at the crown from inside the stone to the outside is possible only if Ø2 is smaller than the critical angle.
On the other hand, all light striking the pavilion facets has to be totally reflected by the pavilion facets. This means, angle δ in equation (1a) has to be larger than the critical angle, so that the minimum limit for δ1 is: δ1 = Øcr = 24.5°. This limit substituted in equation (1a) gives:
|
이것이 다각원형 연마가공 다이어먼드의 반사 성질을 고안 각들 α와 β를 기초로 하여 완전하게 그리고 충분하게 기술한 식이다. 이런 이유로, 식(6)은 브릴리언트 식이라고 부를 수도 있을 것이다.
내부 반사 후에 (α, β)로 고안된 돌을 떠날 수 있는 모든 광선들 Ø2의 각도적인 여유를 알기 위하여, 돌에 들어갈 수 있는 광선들과 들어가는 광선 Ø1의 최대와 최소의 값을 알아내는 것이 중요하다. 사실, 다이어먼드에 대하여, Ø1은 임계각 Øcr = 24.5°보다 클 수 없다. 그러므로, Ø1은 간격 +24.5 ≤ Ø2 ≥ -24.5안에 변할 수 있다는 것을 한눈에 알 수 있다 (≤ 표시는 더 작거나 또는 같다; ≥ 는 더 크거나 같다는 뜻이다). 광선 Ø2에도 분명하게 같은 것이 적용된다. 만약에 광선 Ø2가 돌을 떠난다고 한다면, 같은 간격 +24.5 ≤ Ø2 ≥ -24.5 안에서 돌의 내부로부터 패시트에 부딪쳐야 한다. 만약에 Ø2 가 임계각보다 작으면, 돌의 내부로부터 외부로 관부에서의 빛의 변화가 가능하다.
다시 말하면, 퍼빌리언 패시트들에 부딪치는 모든 빛들은 퍼빌리언 패시트들에 의해서 모두 반사되어야 한다. 이것은 식(1a)내에서의 각 δ 는 임계각보다 커야만, δ1에 대한 최소값은 δ1 = Øcr = 24.5°라는 의미이다. 이 최소값을 식(1a)에 치환하면
|
|
|
|
and for Ø1:
|
그리고 Ø1에 대하여:
|
|
|
|
Since (α - Øcr) is always positive, angle Ø can actually vary only within an interval (α - Øcr) ≤ Ø ≥ - Øcr in order to warrant total reflection at the pavilion and finally, departure through the crown to the outside.
For a brilliant cut with, say α = 35° and β = 34°, the maximum for Ø will be: Ø1 = α - Øcr = 35 - 24.5 = +10.5°. This substituted into the brilliant equation (6) gives for table reflection (β = 0°) : Ø2 = - 50.5°, which exceeds the critical angle for Ø2. The ray will certainly be reflected by the pavilion (no leakage on this part), but it will not go through the table facet to the outside: it is totally reflected back into the stone. Since the lower limit for Ø2 = -24.5, it follows from equation (6) that only rays that enter with maximum Ø1 = -15.5 (-24.5 = 4 x 35 + 0 -180 - Ø1) can be reflected by the table. The other limit, minimum Ø1 = -24.5 provides Ø2 = -15.5 and -24.5°, which after internal reflection, strike the table from inside with angles Ø2 between -24.5 and -15.5, respectively. All other rays are totally reflected inside the stone or leak through the pavilion.
In s similar way, it follows for table-to-bezel reflection: Ø2 = 4α + β - 180 - Ø1 = 4α + β - 180 - (α - Øcr) = -16.5° for Ø2 (negative sign). The minimum for Ø1 is Ø1 = - 24.5°. In this case, Ø2 results to : Ø2 = +18.5. So, we have for this particular brilliant cut the following limitations:
|
(α - Øcr)은 항상 양수이기 때문에, 모든 광선이 퍼빌리언에서 반사되어 최종적으로 관부를 통하여 외부로 나가기 위해서는, 각 Ø는 실제로는 간격 (α - Øcr) ≤ Ø ≥ - Øcr 의 안에서만 변할 수 있다.
α = 35°와 β = 34°인 다각원형 연마가공을 예로 들면, Ø에 대한 최대각은 Ø1 = α - Øcr = 35 - 24.5 = +10.5°이다. 이것을 브릴리언트 식(6)에 치환하면, 테이블 반사에 대하여 (β = 0°) : Ø2 = - 50.5°이며 Ø2에 대한 임계각을 넘는다. 이 광선은 퍼빌리언에 의해서 확실하게 반사될 것이지만(이 부분에서는 누출이 없다), 테이블 패시트를 통하여 외부로 나가지 않을 것이다: 돌 안으로 완전히 반사되어 버린다. 하한치는 Ø2 = -24.5이므로, 식 (6)에 따라, 최대 Ø1 = -15.5 (-24.5 = 4 x 35 + 0 -180 - Ø1)로 들어가는 광선들만이 테이블에 의해서 반사될 수 있다. 다른 제한치인 최소 Ø1 = -24.5는 Ø2 = -15.5와 -24.5°를 내며, 내부반사 후에 각각 -24.5와 -15.5사이의 각 Ø2들을 지니고 내부로부터 테이블에 부딪친다. 다른 모든 광선들은 돌의 내부로 완전히 반사되거나 또는 퍼빌리언을 통하여 누출된다.
테이블 대 관부사면 반사에도 같은 방법이 적용된다: Ø2에 대하여(음의 부호) Ø2 = 4α + β - 180 - Ø1 = 4α + β - 180 - (α - Øcr) = -16.5°이다. Ø1에 대한 최소는 Ø1 = - 24.5°이다. 이 경우에, Ø2의 결과는 : Ø2 = +18.5이다. 그래서, 다음과 같은 제한을 지닌 특유의 다각원형 연마가공을 얻게 된다.
|
|
Type of reflection
|
Incident ray (Ø1)
|
Departing ray (Ø2)
|
|
max.
|
min.
|
max.
|
min.
|
|
Table to Table
|
-15.5
|
-24.5
|
-15.5(40)
|
-24.5(90)
|
|
Table to Bezel Facet
|
+10.5
|
-24.5
|
+18.5(50)
|
-16.5(43)
|
|
|
반사형태
|
입사 광선 (Ø1)
|
출사 광선 (Ø2)
|
|
max.
|
min.
|
max.
|
min.
|
|
테이블 대 테이블
|
-15.5
|
-24.5
|
-15.5(40)
|
-24.5(90)
|
|
테이블 대 관부사면 패시트
|
+10.5
|
-24.5
|
+18.5(50)
|
-16.5(43)
|
|
|
With these figures the limitations for the ray departing the stone can be calculated by means of the sine law of refraction (sin δ2 = n.sin Ø2) where δ2 is the resultant angle for the direction of a ray outside the stone, which is originated by a ray striking the facet from inside with an angle Ø2. The letter "n" stands for the refractive index of diamond, which is n = 2.41. The angles β2 are given in parenthesis for angles Ø2 in the table above.
|
이 값들로 돌을 떠나는 광선에 대한 제한을 굴절의 sine법칙(sin δ2 = n.sin Ø2)으로 계산할 수 있다. δ2는 돌의 외부방향에 대한 합성 각으로, 각 Ø2로 내부로부터 패시트에 부딪치는 광선에 의해서 생긴다. 문자 "n" 다이어먼드의 굴절률을 표시하며 n = 2.41 이다. 각 β2들은 위의 도표에서 각 Ø2들의 괄호 내에 주어져 있다.
|
|
|
|
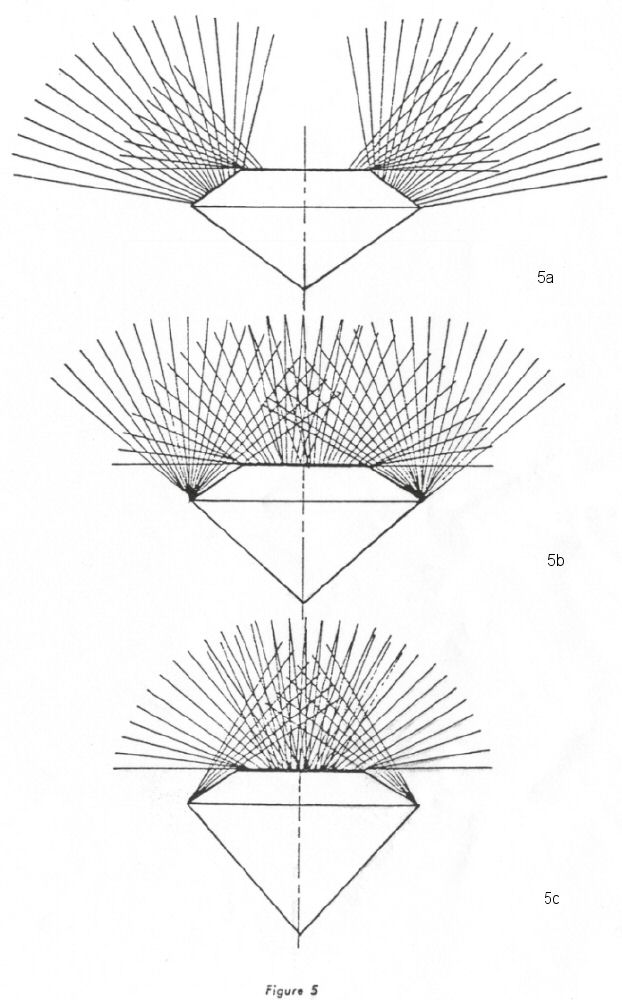
This calculation has been done for three different brilliant designs with α = 35°, 41° and 48°. The crown angle has been assumed the same in all three cases: β = 34°. The effect of possible reflection from each stone has been plotted in Figure 5.
The result, certainly, is very interesting. Figure 5a illustrates a typical fisheye effect with the center of the stone appearing dark. The stone is too flat and the pavilion angle α is too small. The other extreme (α = 48°), (Figure 5c), with the pavilion angle too large, shows a concentration of the reflected rays, particularly from the bezels toward the center. The bezel reflection in this case is very poor; the stone has no fire. It is easy to conceive that the effects of all other cuts must be between the two extremes. Obviously, the most effective cut is represented by Figure 5b, where all radiation comes out of the stone in a sparkling way directed substantially toward the observer.
The transition from the brilliant cut in Figure 5c to that of Figure 5a appears like the unfolding of a rose blossom. In Figure 5c the "rose" is still closed; we have the "rose bud". Such a "bud" certainly has some attractive features, but we have the impression it is not complete yet; we expect the full beauty of the unfolded "blossom". This is what we have in Figure 5b, the beautifully "blossomed rose". Then, the "rose" is fading away (Figure 5a), many "leaves" are lost, and the attractive beauty is gone. With this comparison in mind, the importance of the main angles of a brilliant-cut diamond should be evident.
The basic design of a brilliant and its resultant effect, which has been discussed here, is, of course, modified by the addition of star facets and upper- and lower-girdle facets. All these additional facets also obey the brilliant law, equation (6). The star facets represent bezels with a smaller β-angle, thus providing more white-light reflection. The upper-girdle facets with a larger β add more fire to the stone and the lower-girdle facets represent additional pavilion facets with a modified pavilion angle, thus enhancing the variability of possible reflections. The effect of each variation, and thus the total effect of a brilliant-cut diamond comprising all types of facets, can be calculated with the brilliant equation and plotted in a similar way, as Figure 5.
It can be shown that the application of the brilliant law is not restricted to diamond alone; it can be applied to all other transparent gemstones even to glass and plastics. This law is of general validity, and what we call the degree of brilliancy of a gemstone can also be derived from the brilliant law.
In any case, it should be kept in mind that the brilliant cut of a diamond, actually, is a special optical device like a prism, a lens, a reflector, or a combination of them. The effect of all such devices is the consequence of strict natural laws. There is no mystery behind it. The art of cutting brilliant is not based upon a magic formula that is kept a secret by the cutter. It depends on the individual skill of the cutter to know the natural laws that govern the optical system he is creating, the brilliant, and to approach them to an optimum.
To clarify the physical principles that determine the effect of any cut stone is the foremost intention of this article. What the lens formula is for the lens is the brilliant equation for a brilliant-cut diamond.
|
이 계산은 α = 35°, 41° and 48°의 3 개의 다각원형 고안들에 대하여 이루어졌다. 관부 각은 3 개의 모든 경우들에 대해서 같다고 추정하였다: β = 34°. 각 돌의 반사 가능성의 효과를 그림 5에 그렸다.
결과는 확실히 아주 흥미롭다. 그림 5a는 돌의 중심이 어두운 전형적인 어안(漁眼)효과를 나타낸다. 돌이 너무 납작하며 퍼빌리언 각 α는 너무 작다. 퍼빌리언 각이 너무 큰 다른 극단적인 것 (α = 48°), (그림 5c)는 특히 관부사면들로부터 중심을 향하여 반사 광들의 집중화를 나타낸다. 이 경우에서의 관부사면 반사는 아주 빈약하다; 돌에 불꽃이 없다. 모든 다른 연마가공들의 효과들은 두 개의 극단들 사이에 있어야 한다는 것은 쉽게 상상된다. 명백히, 가장 효과적인 연마가공은 그림 5b에 표현된 것이며, 모든 방사는 충분히 관찰자를 향하여 번쩍거리게끔 돌로부터 나온다.
그림 5c의 다각원형 연마가공으로부터 그림 5a로의 전이는 장미꽃이 점차 피어나는 것같이 보인다. 그림 5c에서 장미 꽃은 아직 피어나지 않았다; 장미 "꽃 봉우리"를 지니고 있다. 그런 꽃 봉우리는 확실히 다소의 매력적인 모습을 지니고 있지만, 아직 완성되지 않았다는 느낌을 지닌다; 우린 아직 피지 않은 "꽃"의 완전한 아름다움을 기대한다. 이것이 그림 5b에 있는 것, 아름답게 핀 장미꽃이다. 그리고 나서, 장미꽃은 점차 시들어(그림 5a), 많은 잎들이 떨어져 매력적인 아름다움이 사라진다. 이 비교를 마음에 새기면, 다각원형 연마가공 다이어먼드의 주요 각들의 중요성은 뚜렷해진다.
여기에서 논의된 브릴리언트의 기본적인 고안과 그 결과적인 효과는 스타 패시트들과 상부와 하부 환상부 패시트들을 더하므로써 물론 수정된다. 이 모든 추가의 패시트들도 역시 브릴리언트 법칙 식(6)을 따른다. 스타 패시트들은 보다 작은 β-각을 지닌 관부사면들을 표현하므로, 더 많은 백색광 반사를 나타낸다. 보다 큰 β를 지닌 상부-환상부 패시트들은 돌에 더욱 많은 불꽃을 더하며, 하부-환상부 패시트들은 수정된 퍼빌리언 각을 지닌 추가적인 퍼빌리언 패시트들을 표현하므로, 가능한 반사들의 변화성을 강화하다. 각 변화의 효과와, 따라서 모든 형태의 패시트들을 포함하고 있는 다각원형 연마가공 다이어먼드의 전체 효과는 브릴리언트 식으로 계산되고 그림 5에서와 같은 방법으로 그려질 수 있다.
브릴리언트 법칙의 적용은 다이어먼드에만 제한되지 않다는 것을 볼 수 있다; 심지어 유리와 플래스틱을 포함한 모든 투명원석들에 적용할 수 있다. 이 법칙의 일반적인 유효성과 원석의 광휘도(brilliancy)라고 하는 것도 역시 브릴리언트 법칙으로부터 유도될 수 있다.
어떠한 경우라도, 다이어먼드의 다각원형 연마가공은 실제로 프리즘, 렌즈, 반사경 또는 그들의 조합과 같은 특별한 광적 도구라는 것을 마음에 새겨 두어야 한다. 그런 모든 도구들의 효과는 엄격한 자연 법칙들의 결과이다. 그 뒤에 감추어진 신비는 없다. 다각원형(brilliant)연마가공의 예술은 연마가공가의 비밀로 감추어진 신비의 공식에 의존하는 것이 아니다. 그가 창조하고 있는 광학 체계를 다스리는 자연의 법칙, 브릴리언트를 알고 있고 그들에 보다 최적화하고자 접근하는 연마가공가의 개인적인 기량에 달려있다.
어떤 연마가공석의 효과를 결정하는 물리적인 원리를 명확하게 하고자 하는 것이 이 논문의 가장 중요한 의도이다. 렌즈를 위한 렌즈공식이라는 것은 다각원형 연마가공 다이어먼드를 위한 브릴리언트(brilliant) 식이다.
|
|
|




